Amistoso Athletic-Mirandés en el centenario del Basconia
Se conmemora el centenario del club vizcaíno de Basauri
Se conmemora el centenario del club vizcaíno de Basauri

Los actos de conmemoración del Bicentenario continúan este domingo con la recreación de la firma de las Actas de Zubieta

El documental reúne los testimonios de 60 personas vinculadas con la historia del campo

El mítico campo de San Mamés cierra sus puertas y dentro de una semanas se abre la nueva sede del Athletic de Bilbao

El documental 'Un siglo y 90 minutos' celebra el centenario del primer partido jugado en San Mamés

Andoni Zubizarreta y Jorge Valdano rinden tributo al desaparecido campo de San Mamés, que hoy habría cumplido cien años

A siete siglos del nacimiento de Boccaccio, los escritores y ensayistas Alberto Manguel y Carlos García Gual reivindican no solo su dimensión literaria, sino también la del pensador y el humanista

Hace 500 años Ponce de León puso un pie en esta península y con él empezó la historia española y europea en Norteamérica.

13 filmes recuerdan la trayectoria de la productora más antigua de Japón

Desde hace 300 años, “limpia, fija y da esplendor” a nuestro idioma, como afirma su lema. Los ilustres miembros de la Real Academia Española (RAE) abren sus puertas a ‘El País Semanal’. Este es un recorrido por las tareas de quienes deciden qué términos merecen entrar en el Diccionario.

Exjugadores y exentrenadores rememoran momentos significativos de la trayectoria del Racing, que ha cumplido 100 años

La formación, cuya plantilla se ha reducido en el último año, actúa este viernes en Almoradí

Exalumnos del Institut del Teatre evocan su experiencia en un montaje por el centenario del centro

El ‘lehendakari’ clausura este miércoles los actos conmemorativos

Urrutia presenta los "pequeños homenajes" que servirán durante el resto de la temporada para celebrar el centenario del campo e ir marcando su despedida

Una web repasa los actos del centenario del teatro donostiarra

2012 fue el centenario de la muerte de uno de los grandes escritores nórdicos. Cerramos su año con su lado más artístico y poético
Uno de los retos para 2013 es aspirar a retomar las relaciones de comercio exterior
Madrid ha recordado con afecto los nacimientos de Georg Solti y John Cage

Con motivo de la Lotería de Navidad, EL PAÍS y la RSME presentan un 'desafío extraordinario' Entre los acertantes se sorteará una biblioteca matemática y un libro con todos los desafíos anteriores

La IAAF celebra los 100 años de su fundación coronando a Usain Bolt como mejor atleta del año por cuarta vez
Cien años de maestros de la costura, un desfile para conmemorar el siglo de historia del hotel Palace de Madrid

Se podrá visitar en sus bodegas una exposición sobre bicentenario de la constitución de 1812

Las luchas entre intelectuales, instituciones y partidos ponen en riesgo la exposición por el centenario del nacimiento del autor de ‘El extranjero’

Faltan unos meses, pero el Teatro del Liceo se adelanta al centenario del compositor en complicidad con la Orquesta y el Coro del Festival de Bayreuth, que interpretarán tres de sus óperas en versión de concierto

Se cumplen cien años del nacimiento del autor de El cuarteto de Alejandría. Una nueva edición recoge en un volumen sus libros sobre Corfú, Rodas y Chipre

Las consideraciones de Lawrence Durrell en su trilogía de las islas resuenan especialmente oportunas en estos momentos

El María Cristina de San Sebastián reabre tras nueve meses de obras para celebrar su centenario Elegancia, estilo y modernidad en un establecimiento emblemático ligado al cine
La Bienal rescata el libro del maestro Otero que fija las reglas de la danza flamenca

El Concurso Internacional de Fuegos Artificiales de San Sebastián hará “un guiño” al Victoria Eugenia por su 100 aniversario

El Palace cumple 100 años como testigo de la historia de la ciudad Sus suites han alojado a Mata Hari o a Bruce Springsteen y escenario de la Guerra Civil o el 23-F
Inaugurado el 12 de octubre de 1912, ha vivido dos repúblicas, una guerra civil y una dictadura, sin olvidar los felices años veinte. Sus paredes han acogido a artistas como Dalí o Ava Gardner.
Resulta sorprendente el desinterés español por reivindicar el importante legado hispano en EE UU
‘Drácula’ no surge de la nada. Stoker reelabora tradiciones del folclore europeo
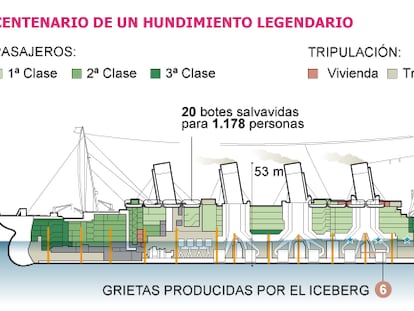
Esta madrugada se cumplió un siglo del hundimiento del barco La catástrofe deviene en la gran metáfora de los peligros de nuestro tiempo

Turing estableció los fundamentos teóricos de la computación y avanzó ideas que varias décadas después de su muerte siguen plenamente vigentes

La Biblioteca Nacional cumple 300 años. Este vídeo muestra la exposición que esta institución ha preparado con el motivo de su aniversario.