El mapamundi de Leonardo

El área del triángulo de Reuleaux (R) de la semana pasada es igual a la del triángulo equilátero de lado 1 (T) más tres veces la del segmento circular (S) que hay sobre cada lado:

R = T + 3S, donde S es el sector circular menos el triángulo:

S = π/6 – T, luego

R = T + 3(π/6 – T) = π/2 – 2T

T = √3/4

R = (π - √3)/2

Algunos lectores han señalado que también hay monedas con forma de polígonos de Reuleaux. La más conocida es, seguramente, la moneda británica de 50 peniques, que es un heptágono de Reuleaux.

La respuesta a la pregunta de si puede haber polígonos de Reuleaux (es decir, de anchura constante) construidos a partir de algunos polígonos irregulares o con un número par de lados, planteada la semana pasada, es afirmativa; pero en este caso los arcos del polígono resultante no serán todos iguales ni con la misma curvatura.

La proyección octante

Uno de los aspectos menos conocidos, pero no por ello menos importante, de las actividades de Leonardo da Vinci son sus contribuciones a la cartografía. En su misceláneo Codex Atlanticus, conservado en la Biblioteca Ambrosiana de Milán, hay un manuscrito de 1508 en el que Leonardo analiza los distintos tipos de proyección cartográfica conocidos en aquella época, como la proyección cónica plana de Tolomeo o el planisferio de Contarini-Rosselli, e introduce una nueva, que consiste en dividir el globo terráqueo en ocho octantes para luego aplanarlos en forma de triángulos de Reuleaux. ¿Fue una elección arbitraria o puramente estética, o el aplanamiento de un octante de esfera produce necesariamente un triángulo de Reuleaux?

Leonardo agrupó los cuatro octantes de cada hemisferio formando una especie de trébol de cuatro hojas, con los polos en los respectivos centros de cada trébol, dando lugar al conocido como “Mapamundi de Leonardo”, aunque su autoría no es segura (algunos piensan que lo dibujó posteriormente uno de sus ayudantes); pero lo que está sólidamente demostrado es que el genio renacentista fue el primero en proponer la proyección en octantes y su agrupación en dos tréboles de cuatro hojas, como lo atestigua, entre otras cosas, un boceto del citado manuscrito de 1508 incluido en el Codex Atlanticus.

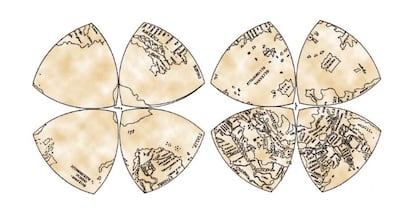
A señalar que la proyección en octantes no es ni conforme ni de igual área. En cartografía, una proyección conforme es la que conserva los ángulos (o al menos la mayoría de ellos), como la proyección de Mercator o la proyección estereográfica, y una proyección de igual área es la que conserva la proporción de las superficies de los distintos países u otras zonas geográficas representadas. Otras características que puede ser conveniente conservar, según el tipo de mapa que se desee confeccionar, son la forma de las distintas zonas geográficas, las distancias, las direcciones…, y a veces conservar una de estas variables implica distorsionar otras. ¿Puede ser una proyección cartográfica a la vez conforme y de igual área? ¿Cómo?

Y, para terminar, les planteo a mis sagaces lectoras y lectores una pregunta que, aunque parezca de botánica, es de pura lógica: ¿Hay tréboles de cuatro hojas?