La circunferencia de los nueve puntos

En las dos últimas semanas hemos hablado de los cuatro “puntos notables” oficiales del triángulo: incentro, circuncentro, ortocentro y baricentro; pero, obviamente, hay otros puntos singulares, como los puntos medios de los lados (M, N, P). Y también son especiales los puntos de intersección de las tres alturas con sus respectivas bases (E, G, J). Y lo que los hace doblemente especiales es que hay una circunferencia que pasa por todos ellos. Y, más difícil todavía, dicha circunferencia también pasa por otros tres puntos singulares, aunque no tan obvios como los anteriores: los puntos medios de los segmentos que unen los tres vértices con el ortocentro (D, F, H).

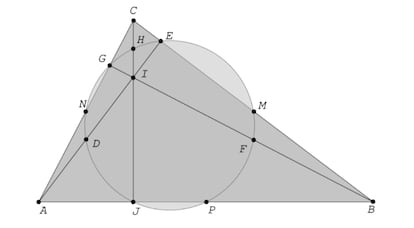
Es la circunferencia de los nueve puntos, también conocida como circunferencia de Feuerbach, por atribuirse su descubrimiento al matemático alemán Karl Wilhelm Feuerbach (1800-1834), hermano del famoso filósofo Ludwig Feuerbach, uno de los padres del materialismo histórico.

La demostración de la existencia de la circunferencia de Feuerbach, así como la determinación de su centro, es algo complicada, pero no requiere más conocimientos que los de la geometría elemental, ¿te atreves a intentarlo? Y si te parece un reto demasiado difícil, puedes empezar por uno más sencillo: demostrar que la circunferencia de Feuerbach de un triángulo es homotética de su circunferencia circunscrita, y que el centro de la homotecia es el ortocentro del triángulo. ¿Cuál es la razón de la homotecia?

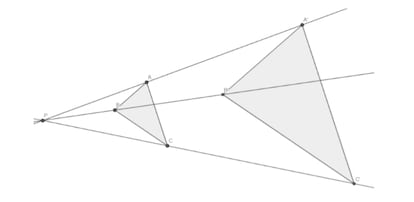
Recordemos que una homotecia es una transformación geométrica con respecto a un punto (P) llamado centro de homotecia, que le hace corresponder a una figura otra semejante (más grande o más pequeña) tal que a todo punto de la primera (A, B, C) le corresponde otro de la segunda (A’, B’, C’) tal que la razón de las distancias de los puntos homólogos al centro, llamada razón de homotecia (k), sea constante:

PA/PA’ = PB/PB’ = PC/PC’ = k

La recta de Euler

Según demostró Leonhard Euler en 1765, el circuncentro, el ortocentro y el baricentro de un triángulo son colineales, es decir, están sobre una misma recta, denominada recta de Euler en honor de su descubridor. Además, el centro de la circunferencia de Feuerbach también se halla sobre la misma recta (¿puedes hallar dónde exactamente?). Y en algunos casos (¿en cuáles?) también el incentro se halla sobre la recta de Euler.

Y la cosa no termina ahí. Otro punto de la recta de Euler que merece un nombre propio es el de Longchamps, llamado así en honor del matemático francés Gaston de Longchamps (1842-1906), que es el simétrico del ortocentro con respecto al circuncentro (¿puedes ver qué es lo que lo hace interesante?).

Y si complicamos un poco más los criterios de determinación de puntos notables de la recta de Euler, nos encontraremos con el punto de Schiffler: dado un triángulo ABC y su incentro I, su punto de Schiffler es aquel en el que concurren las respectivas rectas de Euler de los triángulos ABC, ABI, ACI y BCI (¿puedes determinar su localización exacta, o cuando menos aproximada?).

Y hay más, como el punto de Exeter (descubierto en un taller de matemáticas por ordenador) o el punto far-out, que habrá que dejar para otra entrega. O varias, pues los puntos especiales del aparentemente sencillo polígono de tres lados son tantos que hasta hay una Enciclopedia de Puntos Notables del Triángulo.